Digital Music Programming 2: DC Blocking Filter



This lab demonstrates how to write a program which will filter out unwanted DC components in a soundfile caused by a cheap microphone input or by processing of a soundfile which adds a DC signal to the soundfile.

The Problem

Many cheaper computer microphone inputs add a constant voltage offset to a recorded sound as demonstrated in the figure below:

When processing sound, it is more desirable to have the waveform centered about the zero point; otherwise the sound has a greater chance of clipping, especially if you add several sounds together. Besides, you cannot here 0 Hz, so you do not need to record it. Here is what we actually want, a signal (in this case a sinewave) with no DC component:

The Solution

To get rid of 0 Hz frequencies in the soundfile, it must be filtered. It is possible to subtract a constant amount from every sample in the soundfile, but a more generalized solution which will work in more situations, and work automatically is to filter out the low frequencies.

The simplest and most effect way of filtering out the low frequencies is with the following filter, shown as a flow-graph:

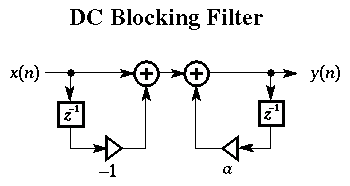Below is a picture of a soundfile on the left which has a noticeable DC offset. The picture of the same sound on the right has been passed through the DC-blocking filter given in the flow-graph above, and it is now centered around rather than above the zero line.

How to convert the flow-graph to an actual program implementation? The flow-graph describes graphically what happens to the input signal as it is filtered. There are three paths the input (and output) to the DC blocking filter make when passing through the filter. The three separate paths of the signal through the flow-graph are highlighted in the picture below:

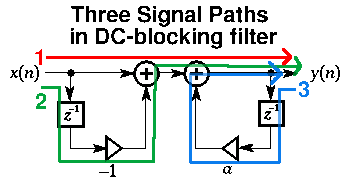After identifying the independent signal paths in the filter, it is easy to write down the difference equation: 

y[n] = x[n] - x[n-1] + a * y[n-1]
Where y[n] is the output at the current time n, and x[n] is the input at the current time n.

Remember in class the steps to figure out how the frequencies are affected by the filter:

Now, with the last equation for the frequency response, the following picture can be generated from the absolute value (or magnitude) of the frequency response:

This picture shows how the frequencies are effected below 400 Hz in a sound sampled at 44.1 kHz. The different plots are related to the scale value a in the flow-graph. When a is close to 1.0, then the filter will only filter out very low frequencies. As a goes toward 0.0, more and more frequencies are noticeable affected by the filter. At a=0.95, the attenuation (lowering of volume) of the sound at 400 Hz would be noticeable since there is a drop of 3dB for sounds in that region of the spectrum.

For musical purposes a is usually set to 0.995 because only frequencies below 30 Hz or so will be significantly reduced, while higher frequencies will remain mostly unaffected by the filter.

A useful analysis of the filter can be done by examining the locations of the poles and zeros on the z-plane. We haven't covered this in class yet, but you can contemplate what the following picture means for next week:

Source Code Example Usage
dcblock.c 


#include "ext.h"
#include "z_dsp.h"

typedef struct {
   t_pxobject msp_data;
   float      lastinput;
   float      lastoutput;
   float      gain;
} MyObject;

void* object_data;

void   main            (void);
void*  create_object   (void);
void   MessageDSP      (MyObject* mo, t_signal** signal, short* count);
void   MessageClear    (MyObject* mo);
t_int* Perform         (t_int *parameters);

void main(void) {
   setup((t_messlist**)&object_data, (method)create_object, (method)dsp_free,
         (short)sizeof(MyObject), NULL, A_NOTHING);
   addmess((method)MessageDSP,   "dsp",   A_CANT, A_NOTHING);
   addmess((method)MessageClear, "clear", A_NOTHING);
   dsp_initclass();
}

void* create_object(void) {
   MyObject *mo = (MyObject*)newobject(object_data);
   dsp_setup((t_pxobject*)mo, 1);
   outlet_new((t_pxobject*)mo, "signal");
   mo->gain = 0.995;
   MessageClear(mo);
   return mo;
}

void MessageDSP(MyObject* mo, t_signal** signal, short* count) {
   #pragma unused(count)
   dsp_add(Perform, 5, 5, mo, signal[0]->s_vec, signal[1]->s_vec, signal[0]->s_n);
}

void MessageClear(MyObject *mo) {
   mo->lastinput  = 0.0;
   mo->lastoutput = 0.0;
}

t_int* Perform(t_int *parameters) {
   long      pcount = (long)     (parameters[1]);
   MyObject *mo     = (MyObject*)(parameters[2]);
   t_float  *input  = (t_float*) (parameters[3]);
   t_float  *output = (t_float*) (parameters[4]);
   long      count  = (long)     (parameters[5]);
   long      i;

   for (i=0; i<count; i++) {
      output[i] = input[i] - mo->lastinput + mo->gain * mo->lastoutput;
      mo->lastinput  = input[i];
      mo->lastoutput = output[i];
   }

   return parameters+pcount+1;
}

Exercises

  1. compile the dcblock~ filter object.

  2. Here is a soundfile with a DC offset: 440hzoffset.wav. Filter it with the MSP object you just compiled. Listen to the soundfile and then to the output soundfile. Do they sound the same or different? Look at the input and output soundfiles in Peak. How do the soundfiles compare to each other visually inside of Peak? If you are using the computer lab next to the cafeteria, you can use SoundHack instead of Peak.

  3. Make the feedback filter gain, a, an input parameter into the dcblock~ object.

  4. Try different amounts of feedback gain and see how it affects a whitenoise soundfile (try whitenoise.wav or make your own continuous whitenoise with the rand~ MSP object used as the input to the DC-blocking filter. Use values in the range from [-1.0 .. +1.0] for the feedback gain.

  5. Add a DC offset of 2.0 to a signal. Listen to the signal directly through the dac~ object. Now put the DC offset signal into the DC-blocking filter just before the signal is sent to the dac~ object. How does the sound change? Here are the two configurations to try: