Synthesis Theory I: Assignment 5



1. (a) Draw the spectrum for the following pole-zero diagram (The spectrum of the output sound if white noise were used as the input).
(b) If the sampling rate were 44.1 kHz, at what frequency (approximately, of course) would the above filter resonate?
2. What is the formula for Euler's Identity?
3. What is the advantage of using a complex sinusoid to measure the spectrum of a signal (as opposed to a single real sinusoid such as a sine, or cosine wave)?
4. Here is a short audio signal which continuously repeats: 
    0.6, 0.14, -0.2, -0.14, -0.2, -0.14, -0.2, 0.14
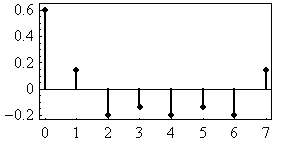This signal only contains cosine sinusoids, so you will not have to measure the signal with complex sinusoids. There are five distinct possible frequencies in this signal: 0 Hz, fs/8, fs/4, 3 fs/8, and fs/2. Here are the time-series for each frequency: 
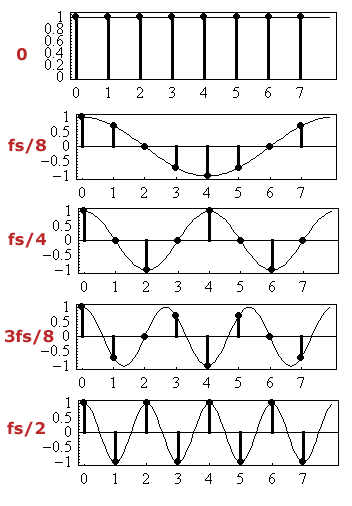
   0 Hz   =  1,  1,     1,    1,      1,  1,     1,  1
   fs/8   =  1,  0.707, 0,   -0.707, -1, -0.707, 0,  0.707
   fs/4   =  1,  0,    -1,    0,      1,  0,    -1,  0
   3 fs/8 =  1, -0.707, 0,    0.707, -1,  0.707, 0, -0.707
   fs/2   =  1, -1,     1,   -1,      1, -1,     1, -1
Here is a plot of each possible sinewave:
(a) Draw the 5-point spectrum of the signal by extracting the amplitudes of the 5 sinusoids present in the signal. Here are some of the amplitudes: 
   0 Hz    = 0
   fs/8    = ???
   fs/4    = 0.2  
   3 fs/8  = ???
   fs/2    = 0

(b) What are the amplitudes of the of the fs/8 and 3fs/8 frequencies present in the signal? The normalization factor is 4 (divide by 4 after summing the multiplied signals) to get the correct initial amplitudes. Check your answers by calculating the fs/4 frequency and see if you get 0.2 as the initial amplitude.

(c) Verify that either the frequency 0 Hz or fs/2 have an amplitude of 0 in the signal.

(d) For extra credit, demonstrate that the amplitudes of the frequencies in the spectrum you calculated in part (b) can be used to generate the original sequence: 

    0.6, 0.14, -0.2, -0.14, -0.2, -0.14, -0.2, 0.14
In other words, what are the sequences of sampled values from the three (co)sinewaves that add up to generate the final signal?