Equivalence of Flowgraphs and Difference Equations

The following figure shows a flowgraph of a filter which contains one zero and one pole. This flowgraph can be converted to a difference equation by examining the path of the signal through the filter. For this filter, there are three possible paths for the signal to reach the output. x indicates the signal entering the filter, and y indicates the filtered signal leaving the filter.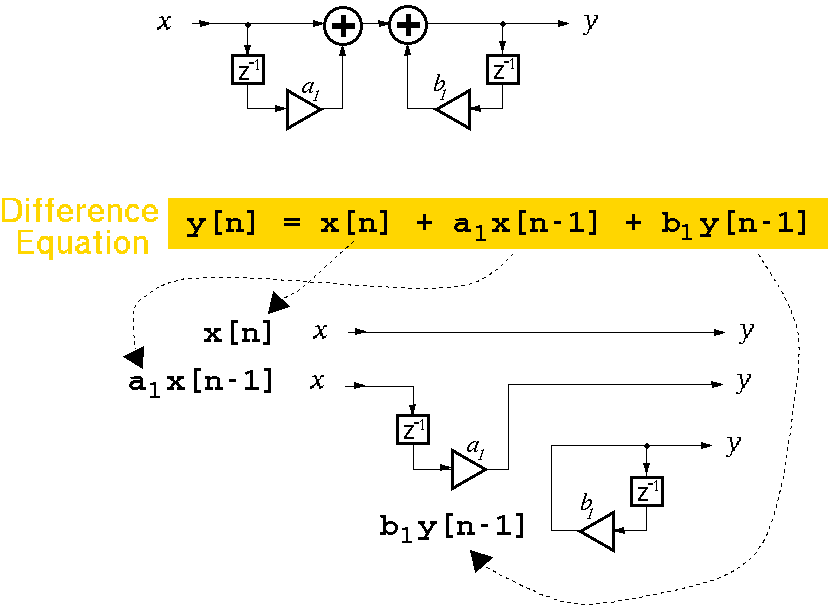

The first path of the signal is direct from left to right. There are no delays or gains affecting the direct signal through the filter on this path, so the algebraic term for this piece is very simple: x[n].   x[n] means the value at time n of the input signal x, where n is the time index.

The second path is through the feedforward delay at the left of the flowgraph. Going along this path, notice two element: a delay and a scale (by a₁). Thus the signal component going through the second path yields the algebraic expression:   a₁ x[n-1]. The delay is indicated by x[n-1] which means that the previous sample, since x[n] can be thought of as the current sample. n is the unit of time, so n-1 is the previous instant of time. The value a₁ is multiplied by the previous input sample value since it is a constant gain on the signal going through the feedforward delay.

The last signal path is a feedback from the output of the filter and is not directly associated with the signal input -- only the signal output. The algebraic expression for the feedback portion of the filter is:  b₁ y[n-1]. The current output can be considered to be y[n]. Thus, the value y[n-1] is the previous output from the filter. The feedback path contains a gain of b₁ which is multiplied by the previous output to generate the third signal component: b₁ y[n-1].

Now you should be able to figure out how to convert a flowgraph (in its generalize form) into a difference equation which can be implemented in a program written in a language such as C.