Digital Music Programming 2: Homework 4: allpass filtersThe goal of this homework is to implement an allpass filter, which has a difference equation of: y[n] = -g x[n] + x[n-1] + g y[n-1] where y is the output signal, x is the input signal, and g is the feedback gain. This is called a first-order allpass filter, because it only uses a one sample delay. It is possible to create second order allpass filters using up to a two-sample delay. Any-order allpass filters can be created by using an arbitrary amount of maximum delay. The interesting thing about the allpass filter (of any order) is that the amplitudes of the frequencies are not changed as the sound travels through the filter. This may seem like a boring filter, but what does change is the time that it takes for different frequencies to get through the filter. Here is a plot of the group delay for the filter which describes how the sound is delays at various frequences and values of g, the gain. 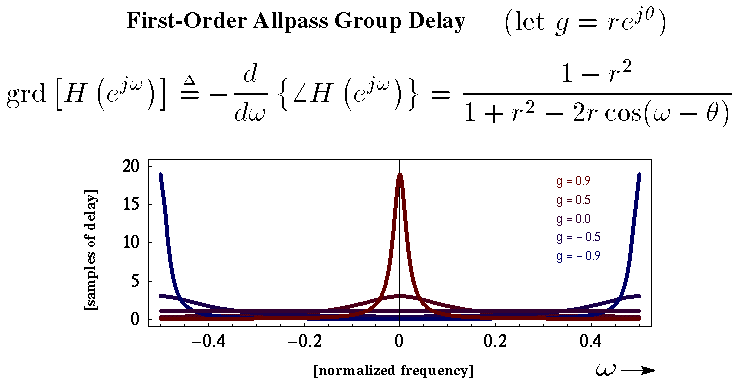
Interesting note: water behaves as an allpass filter. Over long distances, the high frequencies will arrive sooner than lower frequencies. So you can hear thunder underwater from hundreds of miles away which sounds like a sinewave falling in pitch. This is called dispersion. Here are some soundfiles which magnify the effect of the first order allpass several hundred times to make the frequency delays noticeable: [ dispersion of whitenoise | dispersion of whitenoise | dispersion of voice | dispersion of voice ] Assignment:
|